How To Read Pearls of Functional Algorithm Design

Ever felt more ignorant the further you get into a book?

Pearls of Functional Algorithm Design is one of those. Lots of people are mystified by this book too, so it’s not just you. Moreover, it’s not the book’s fault either because it’s written for a very select readership.

It turns out that even if you’re not inside that select readership, there’s a kind of secret deciphering key that allows you to extract the best parts.

The big picture is explained in 4 key sentences in the 1st paragraph on the 2nd page of the Preface (page x):

Many, though by no means all, of the pearls start with a specification in Haskell and then go on to calculate a more efficient version.

This is the 1st of 4 key sentences. This is software engineering turned into a science as much as an art. Variously known as make it Work, make it Right, make it Fast, and as Compile, Conform, Perform; the classical principle at its core is just 2 steps: Make it Right; Then and only then, Make it Faaaaast!

So how to make it right?

Here’s how: Take the spec in English and pretty much translate it word-for-word into Haskell. Translate the spec into what’s obviously the spec. Make obvious that there are Obviously No Bugs.

There are two ways to write code: write code so simple there are obviously no bugs in it, or write code so complex that there are no obvious bugs in it. — Tony Hoare

Then what? The book goes on to say:

My aim in writing these particular pearls is to see to what extent algorithm design can be cast in a familiar mathematical tradition of calculating a result by using well-established mathematical principles, theorems and laws.

We’ve got something Right. Now how to make it Fast?

Answer: CALCULATE!

Remember those math word problems which require you to set up a system of linear equations? And you then fiddle with the x’s and y’s until out pops the solution?

Same idea, except that you start with the Obviously-No-Bugs code as if it were a bunch of linear equations. You then subtitute equals for equals, swizzling the code around until you get the solution. Which in this case is a faster version.

What’s an example like? Well, the book has many, many finely crafted examples. The problem is that each one of them presumes deep background on the part of the reader.

Pearls of Functional Algorithm Design is sooooo not a beginner’s book.

Sucks :(

But it’s priced affordably and the title is inviting and many people buy it and find out to their chagrin that it’s not what they were looking for. Not uncommon: another book that suffers the same fate is Purely Functional Data Structures.

Still, we can ask: What does Faster-Code look like? How does it compare to Obviously-No-Bugs?

And the answer is:

While it is generally true in mathematics that calculations are designed to simplify complicated things, in algorithm design it is usually the other way around: simple but inefficient programs are transformed into more efficient versions that can be completely opaque.

So Faster-Code is no longer Obviously-No-Bugs. In fact, FC looks so different from ONB that no genius eyeballing can tell it’s one and the same program!

Compare before:

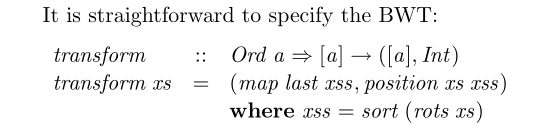
and after:

But just like we learned waaaaay back when doing those word problems: as long as we are careful with the swizzling (here, program transformations) we’re guaranteed to arrive at right answer.

In other words, when swizzling and swooshing around in the CALCULATE! step, the program transformations must preserve correctness.

The book drives home what’s really at stake here:

“It is not the final program that is the pearl; rather it is the calculation that yields it.”

This 4th and last sentence is missed by lots of people. They scratch their heads wondering what these fibonacci-wannabe case studies have to do with The Real World. The key point they’ve missed out on: next-generation program optimizations.

You might have noticed that computers today gulp down humongous linear equations for breakfast.

Indeed, you probably have already spotted the outline of a holy grail: Start with Obviously-No-Bugs and a compiler of the future would swoosh it around to arrive at Faster-Code.

“But aren’t we already there with today’s optimizing compilers?” you might ask.

Nope.

Current compilers deploy only last-mile optimizations, crunching on various fully-imperative, semi-portable assembly languages. The usual suspects are SSA form, LLVM’s IR, and GCC’s RTL.

In contrast, the book is a grab-bag of ultra-high-level optimizations in the realm of pure and lazy languages. These languages are as different as can be from assembly language. And the conspicuous inhabitant of this realm is Haskell, which is used for all of the book’s source-to-source transformations.

Which isn’t to say that the compiler of the future neglects all of the research into low-level optimizations. No reason not to apply both high- and low-level techniques, but the feel is that most of the low-lying fruit has been plucked already, so the only way to go is up.

And it’s damnedly hard to go up in imperative languages because of the sequentialism imposed by the von Neumann execution model.

John Backus in his 1977 Turing Award Lecture critiques the bottlenecks of the von Neumann model and proposes an alternative centered around functional languages.

But the path is a rocky one. A big criticism of this CALCULATE! research program is how the transformations depend on a flash of insight, an Eureka step. No-one has any idea how to program Eurekas into a compiler. So much for the comparison to brute-force number crunching.

Anyway, so now that

You’ve bought the book, how can you make the best of it?

Here are some activities you could do with the book, in decreasing order of difficulty:

1. Make a table classifying each pearl based on any pattern you might have noticed. Tags you could use:

   • generate-and-test problems
   • using divide-and-conquer to provide speed boost
   • data structure optimizations, e.g. replace lists with something else)
   • tail-call optimization
   • straightforward vs gnarlier translation of problem into Haskell
   • detailed vs skimpy calculation steps
   • eureka-ish vs automatable calculations

2. What invariants do any of the functions satisfy? Hack together some quickcheck properties for the interesting ones. For starters, pearl no. 23 on the convex hull actually uses quickcheck. But it’s the only one in the book.

3. Make a table where the left column describes the problem and the right column gives the Obviously-No-Bugs translation into Haskell. Bonus points for a third column translating the code into ordinary spoken English.

4. Last but not least, observe the code closely. The book collects together many, many fine specimens of the distinguished Oxford school of Haskell.

Let me expand on the last point: Zed Shaw publishes a popular and hugely effective series of intro programming books where he encourages the reader to type in the code samples, rather than merely downloading them from a website. As he writes in his seminal Learn Python The Hard Way,

Typing the code samples and getting them to run will help you learn the names of the symbols, get familiar with typing them, and get you reading the language. — Zed Shaw

I’d even go out on a limb and suggest that like professional athletes, programmers use muscle memory and hand-eye coordination in ways not well understood.

In a nutshell, if you’re struggling to get better at writing beautiful, idiomatic Haskell, and you’ve had enough of these inner whisperings:

• I’m just not confident writing Haskell code
• I always feel I’m writing stupid code
• There must be a more elegant way still eluding me

then one way to level up with utterly zero prereqs is to type out the code in this book and immerse yourself in the high-gloss elegance of Richard Bird’s pearls.

Even if you don’t understand any of them yet.

---

Kim-Ee Yeoh hacks haskell for fun, profit, and greater good by doing 4 things: He reads, he writes, he learns, and he teaches.